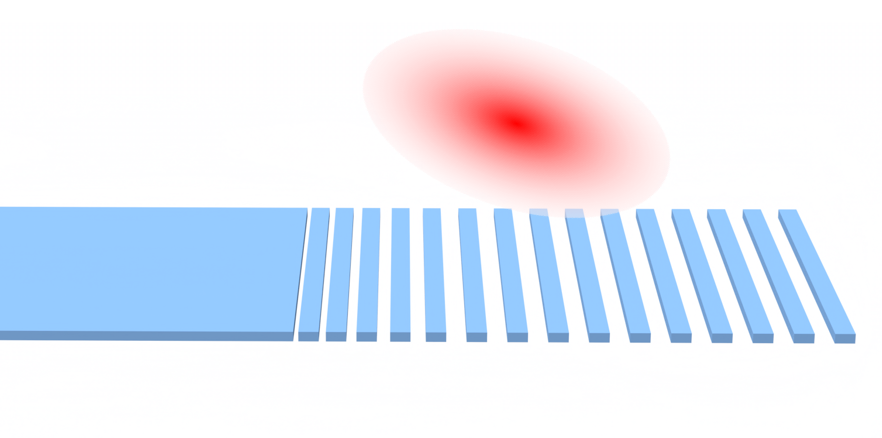
The cost of running the entire optimization is about 8 FlexCredit (check this)
In this tutorial, we will show how to perform the adjoint-based inverse design of a quantum emitter (QE) light extraction structure. We will use a PointDipole to model the QE embedded within an integrated dielectric waveguide. Then, we will build an optimization problem to maximize the extraction efficiency of the dipole radiation into a collection waveguide. In addition, we will show how to use FieldMonitor objects in adjoint simulations to calculate the flux radiated from the dipole. You can also find helpful information in this related notebook.
If you are unfamiliar with inverse design, we recommend the inverse design lectures and this introductory tutorial.
Let's start by importing the Python libraries used throughout this notebook.
# Standard python imports.
import pickle
from typing import List
# Import autograd for automatic differentiation.
import autograd as ag
import autograd.numpy as anp
import matplotlib.pylab as plt
import numpy as np
import optax
import scipy as sp
# Import regular tidy3d.
import tidy3d as td
import tidy3d.web as web
from tidy3d.plugins.autograd import (
make_erosion_dilation_penalty,
make_filter_and_project,
rescale,
value_and_grad,
)
Simulation Set Up¶
The coupling region (design region) extends a single-mode dielectric waveguide placed over a lower refractive index substrate. The QE is modeled as a PointDipole oriented in the y-direction. The QE is placed within the design region so we surround it with a constant refractive index region to protect it from etching.
# Geometric parameters.
cr_w = 1.0 # Coupling region width (um).
cr_l = 3.0 # Coupling region length (um).
wg_thick = 0.19 # Collection waveguide thickness (um).
wg_width = 0.35 # Collection waveguide width (um).
wg_length = 1.0 # Collection waveguide length (um).
# Material.
n_wg = 3.50 # Structure refractive index.
n_sub = 1.44 # Substrate refractive index.
# Fabrication constraints.
min_feature = 0.06 # Minimum feature size.
non_etch_r = 0.06 # Non-etched circular region radius (um).
# Inverse design set up parameters.
grid_size = 0.015 # Simulation grid size on design region (um).
max_iter = 100 # Maximum number of iterations.
iter_steps = 5 # Beta is increased at each iter_steps.
beta_min = 1.0 # Minimum value for the tanh projection parameter.
learning_rate = 0.02
# Simulation wavelength.
wl = 0.94 # Central simulation wavelength (um).
bw = 0.04 # Simulation bandwidth (um).
n_wl = 41 # Number of wavelength points within the bandwidth.
Let's calculate some variables used throughout the notebook. Here, we will also define the QE position and monitor planes.
# Minimum and maximum values of the permittivity.
eps_max = n_wg**2
eps_min = 1.0
# Material definition.
mat_wg = td.Medium(permittivity=eps_max)
mat_sub = td.Medium(permittivity=n_sub**2)
# Wavelengths and frequencies.
wl_max = wl + bw / 2
wl_min = wl - bw / 2
wl_range = np.linspace(wl_min, wl_max, n_wl)
freq = td.C_0 / wl
freqs = td.C_0 / wl_range
freqw = 0.5 * (freqs[0] - freqs[-1])
run_time = 3e-12
# Computational domain size.
pml_spacing = 0.6 * wl
size_x = wg_length + cr_l + pml_spacing
size_y = cr_w + 2 * pml_spacing
size_z = wg_thick + 2 * pml_spacing
eff_inf = 10
# Source position and monitor planes.
cr_center_x = wg_length + cr_l / 2
qe_pos = td.Box(center=(cr_center_x - 0.5, 0, 0), size=(0, 0, 0))
qe_field_plan = td.Box.surfaces(center=(cr_center_x, 0, 0), size=(cr_l, cr_w, 2 * wg_thick))
wg_mode_plan = td.Box(center=(wl / 4, 0, 0), size=(0, 4 * wg_width, 5 * wg_thick))
# Number of points on design grid.
nx_grid = int(cr_l / grid_size)
ny_grid = int(cr_w / grid_size / 2)
# xy coordinates of design grid.
x_grid = np.linspace(cr_center_x - cr_l / 2, cr_center_x + cr_l / 2, nx_grid)
y_grid = np.linspace(0, cr_w / 2, ny_grid)
Optimization Set Up¶
We will start defining the density-based optimization functions to transform the design parameters into permittivity values. Here we include the ConicFilter, where we impose a minimum feature size fabrication constraint, and the tangent hyperbolic projection function, eliminating intermediary permittivity values as we increase the projection parameter beta. You can find more information in the Inverse design optimization of a compact grating coupler.
def pre_process(params, beta):
filter_project = make_filter_and_project(
radius=min_feature, dl=grid_size, beta=beta, eta=0.5, filter_type="conic"
)
params1 = filter_project(params, beta)
return params1
def get_eps(params, beta: float = 1.00):
"""Returns the permittivities after filter and projection transformations"""
params1 = pre_process(params, beta=beta)
eps = eps_min + (eps_max - eps_min) * params1
eps = anp.maximum(eps, eps_min)
eps = anp.minimum(eps, eps_max)
return eps
This function includes a circular region of constant permittivity value surrounding the QE. The objective here is to protect the QE from etching. In applications such as single photon sources, a larger unperturbed region surrounding the QE can be helpful to reduce linewidth broadening, as stated in J. Liu, K. Konthasinghe, M. Davanco, J. Lawall, V. Anant, V. Verma, R. Mirin, S. Nam, S. Woo, D. Jin, B. Ma, Z. Chen, H. Ni, Z. Niu, K. Srinivasan, "Single Self-Assembled InAs/GaAs Quantum Dots in Photonic Nanostructures: The Role of Nanofabrication," Phys. Rev. Appl. 9(6), 064019 (2018) DOI: 10.1103/PhysRevApplied.9.064019.
def include_constant_regions(eps, circ_center=[0, 0], circ_radius=1.0):
# Build the geometric mask.
yv, xv = anp.meshgrid(y_grid, x_grid)
# Shouldn't this be --> |x-x0|^2 + |y-y0|^2 <= r*2
geo_mask = (
anp.where(
anp.abs((xv - circ_center[0]) ** 2 + (yv - circ_center[1]) ** 2) <= (circ_radius**2),
1,
0,
)
* eps_max
)
eps = anp.maximum(geo_mask, eps)
return eps
Now, we define a function to update the td.CustomMedium using the permittivity distribution. The simulation will include mirror symmetry concerning the y-direction, so only the upper half of the design region is returned by this function during the optimization process. To get the whole structure, you need to set unfold=True.
def update_design(eps, unfold=False) -> List[td.Structure]:
# Definition of the coordinates x,y along the design region.
coords_x = [(cr_center_x - cr_l / 2) + ix * grid_size for ix in range(nx_grid)]
eps_val = anp.array(eps).reshape((nx_grid, ny_grid, 1))
if not unfold:
coords_yp = [0 + iy * grid_size for iy in range(ny_grid)]
coords = dict(x=coords_x, y=coords_yp, z=[0])
eps1 = td.SpatialDataArray(eps_val, coords)
eps_medium = td.CustomMedium(permittivity=eps1)
box = td.Box(center=(cr_center_x, cr_w / 4, 0), size=(cr_l, cr_w / 2, wg_thick))
structure = [td.Structure(geometry=box, medium=eps_medium)]
# VJP for one of anp.copy(), anp.concatenate(), or anp.fliplr() not defined,
# so the optimization should only be run with `unfold=False` for now
else:
coords_y = [-cr_w / 2 + iy * grid_size for iy in range(2 * ny_grid)]
coords = dict(x=coords_x, y=coords_y, z=[0])
eps1 = td.SpatialDataArray(
anp.concatenate((anp.fliplr(anp.copy(eps_val)), eps_val), axis=1), coords
)
eps_medium = td.CustomMedium(permittivity=eps1)
box = td.Box(center=(cr_center_x, 0, 0), size=(cr_l, cr_w, wg_thick))
structure = [td.Structure(geometry=box, medium=eps_medium)]
return structure
In the next cell, we define the output waveguide and the substrate, as well as the simulation monitors. It is worth mentioning the inclusion of a ModeMonitor in the output waveguide and a FieldMonitor box surrounding the dipole source to calculate the total radiated power.
# Input/output waveguide.
waveguide = td.Structure(
geometry=td.Box.from_bounds(
rmin=(-eff_inf, -wg_width / 2, -wg_thick / 2),
rmax=(wg_length, wg_width / 2, wg_thick / 2),
),
medium=mat_wg,
)
# Substrate layer.
substrate = td.Structure(
geometry=td.Box.from_bounds(
rmin=(-eff_inf, -eff_inf, -eff_inf), rmax=(eff_inf, eff_inf, -wg_thick / 2)
),
medium=mat_sub,
)
# Point dipole source located at the center of TiO2 thin film.
dp_source = td.PointDipole(
center=qe_pos.center,
source_time=td.GaussianPulse(freq0=freq, fwidth=freqw),
polarization="Ey",
)
# Mode monitor to compute the FOM.
mode_spec = td.ModeSpec(num_modes=1, target_neff=n_wg)
mode_monitor_fom = td.ModeMonitor(
center=wg_mode_plan.center,
size=wg_mode_plan.size,
freqs=[freq],
mode_spec=mode_spec,
name="mode_monitor_fom",
)
# Field monitor to compute the FOM.
field_monitor_fom = []
for i, plane in enumerate(qe_field_plan):
field_monitor_fom.append(
td.FieldMonitor(
center=plane.center,
size=plane.size,
freqs=[freq],
name=f"field_monitor_fom_{i}",
)
)
# Mode monitor to compute spectral response.
mode_spec = td.ModeSpec(num_modes=1, target_neff=n_wg)
mode_monitor = td.ModeMonitor(
center=wg_mode_plan.center,
size=wg_mode_plan.size,
freqs=freqs,
mode_spec=mode_spec,
name="mode_monitor",
)
# Field monitor to compute spectral response.
field_monitor = []
for i, plane in enumerate(qe_field_plan):
field_monitor.append(
td.FieldMonitor(
center=plane.center, size=plane.size, freqs=freqs, name=f"field_monitor_{i}"
)
)
# Field monitor to visualize the fields.
field_monitor_xy = td.FieldMonitor(
center=(size_x / 2, 0, 0),
size=(size_x, size_y, 0),
freqs=freqs,
name="field_xy",
)
Lastly, we have a function that receives the design parameters from the optimization algorithm and then gathers the simulation objects altogether to create a td.Simulation.
def make_adjoint_sim(param, beta: float = 1.00, unfold=False):
eps = get_eps(param, beta)
eps = include_constant_regions(
eps, circ_center=[qe_pos.center[0], qe_pos.center[1]], circ_radius=non_etch_r
)
structure = update_design(eps, unfold=unfold)
# Creates a uniform mesh for the design region.
adjoint_dr_mesh = td.MeshOverrideStructure(
geometry=td.Box(center=(cr_center_x, 0, 0), size=(cr_w, cr_l, wg_thick)),
dl=[grid_size, grid_size, grid_size],
enforce=True,
)
grid_spec = td.GridSpec.auto(
wavelength=wl_max,
min_steps_per_wvl=15,
override_structures=[adjoint_dr_mesh],
)
return td.Simulation(
size=[size_x, size_y, size_z],
center=[size_x / 2, 0, 0],
grid_spec=grid_spec,
symmetry=(0, -1, 0),
structures=[substrate, waveguide] + structure,
sources=[dp_source],
monitors=[field_monitor_xy, mode_monitor_fom] + field_monitor_fom,
run_time=run_time,
subpixel=True,
)
Initial Light Extractor Structure¶
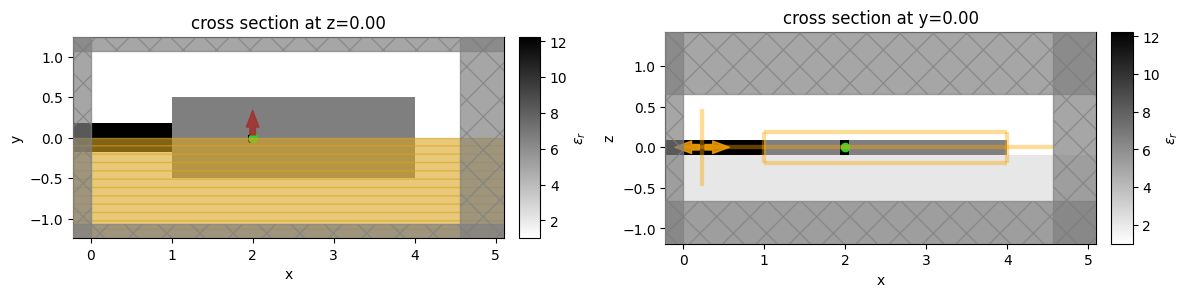
Let's create a uniform initial permittivity distribution and verify if all the simulation objects are in the correct places.
init_par = np.ones((nx_grid, ny_grid)) * 0.5
init_design = make_adjoint_sim(init_par, beta=beta_min, unfold=True)
fig, (ax1, ax2) = plt.subplots(1, 2, tight_layout=True, figsize=(12, 4))
init_design.plot_eps(z=0, ax=ax1, monitor_alpha=0.0)
init_design.plot_eps(y=0, ax=ax2)
plt.show()
We will also look at the collection waveguide mode to ensure we have considered the correct one in the ModeMonitor setup. We use the ModeSolver plugin to calculate the first two waveguide modes, as below.
from tidy3d.plugins.mode import ModeSolver
from tidy3d.plugins.mode.web import run as run_mode_solver
sim_init = init_design.updated_copy(monitors=[field_monitor_xy, mode_monitor] + field_monitor)
mode_solver = ModeSolver(
simulation=sim_init,
plane=wg_mode_plan,
mode_spec=td.ModeSpec(num_modes=2),
freqs=[freq],
)
modes = run_mode_solver(mode_solver, reduce_simulation=True)
16:10:23 CEST Mode solver created with task_id='fdve-65e65354-aedf-458c-a514-a7eccc5e4b24', solver_id='mo-581ee868-4940-489c-bab0-2c43f11c8df2'.
Output()
Output()
16:10:26 CEST Mode solver status: queued
16:10:28 CEST Mode solver status: running
16:10:32 CEST Mode solver status: success
Output()
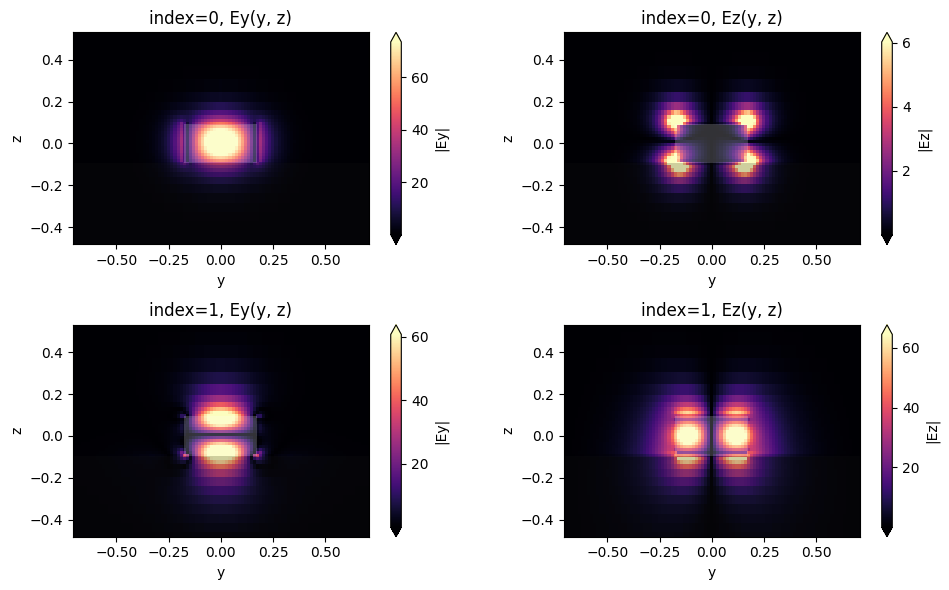
After inspecting the mode field distribution, we can confirm that the fundamental waveguide mode is mainly oriented in the y-direction, thus matching the dipole orientation.
fig, axs = plt.subplots(2, 2, figsize=(10, 6), tight_layout=True)
for mode_ind in range(2):
for field_ind, field_name in enumerate(("Ey", "Ez")):
ax = axs[mode_ind, field_ind]
mode_solver.plot_field(field_name, "abs", mode_index=mode_ind, f=freq, ax=ax)
ax.set_title(f"index={mode_ind}, {field_name}(y, z)")
Then, we will calculate the initial coupling efficiency to see how this random structure performs.
sim_data = web.run(sim_init, task_name="initial QE light extractor (Autograd)")
16:10:35 CEST Created task 'initial QE light extractor (Autograd)' with task_id 'fdve-4ca772ae-badc-4827-8da8-4b32cf325ab4' and task_type 'FDTD'.
View task using web UI at 'https://tidy3d.simulation.cloud/workbench?taskId=fdve-4ca772ae-ba dc-4827-8da8-4b32cf325ab4'.
Task folder: 'default'.
Output()
16:10:37 CEST Maximum FlexCredit cost: 0.060. Minimum cost depends on task execution details. Use 'web.real_cost(task_id)' to get the billed FlexCredit cost after a simulation run.
16:10:38 CEST status = success
Output()
16:10:43 CEST loading simulation from simulation_data.hdf5
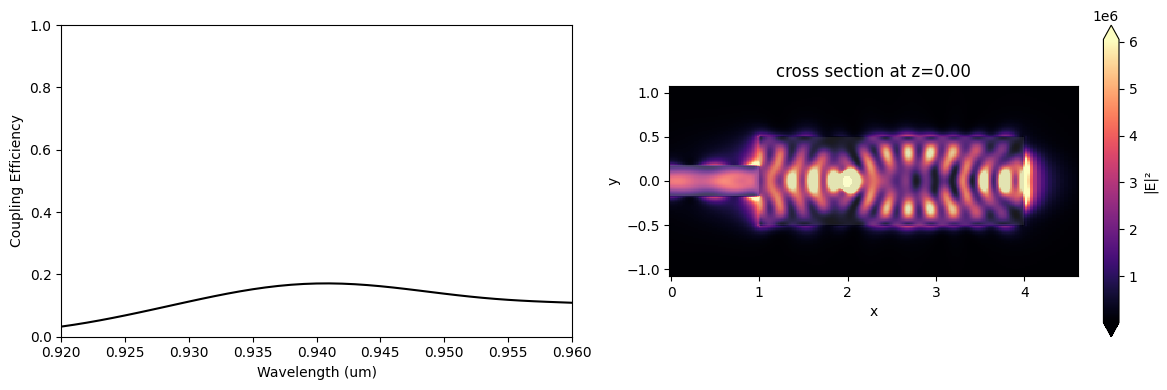
The modal coupling efficiency is normalized by the dipole power. That is necessary because the dipole power will likely change significantly when the optimization algorithm modifies the design region.
mode_amps = sim_data["mode_monitor"].amps.sel(direction="-", mode_index=0)
mode_power = np.abs(mode_amps) ** 2
dip_power = np.zeros(n_wl)
for i in range(len(field_monitor)):
field_mon = sim_data[f"field_monitor_{i}"]
dip_power += np.abs(field_mon.flux)
coup_eff = mode_power / dip_power
f, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 4), tight_layout=True)
ax1.plot(wl_range, coup_eff, "-k")
ax1.set_xlabel("Wavelength (um)")
ax1.set_ylabel("Coupling Efficiency")
ax1.set_ylim(0, 1)
ax1.set_xlim(wl - bw / 2, wl + bw / 2)
sim_data.plot_field("field_xy", "E", "abs^2", z=0, ax=ax2, f=freq)
plt.show()
Optimization¶
The objective function defined next is the device figure-of-merit (FOM) minus a fabrication penalty.
# Figure of Merit (FOM) calculation.
def fom(sim_data: td.SimulationData) -> float:
"""Return the coupling efficiency."""
# best to use autograd-wrapped numpy functions for differentiation
mode_amps = sim_data["mode_monitor_fom"].amps.sel(direction="-", f=freq, mode_index=0).data
mode_power = anp.sum(anp.abs(mode_amps) ** 2)
# unlike Jax version, should avoid in-place operators (e.g, `+=`), use numpy when possible
field_mon_list = [sim_data[f"field_monitor_fom_{i}"] for i in range(0, 6)]
dip_power = anp.sum([anp.abs(mon.flux.data) for mon in field_mon_list])
return mode_power, dip_power
def penalty(params, beta) -> float:
"""Penalize changes in structure after erosion and dilation to enforce larger feature sizes."""
params_processed = pre_process(params, beta=beta)
erode_dilate_penalty = make_erosion_dilation_penalty(radius=min_feature, dl=grid_size)
ed_penalty = erode_dilate_penalty(params_processed)
return ed_penalty
# Objective function to be passed to the optimization algorithm.
def obj(param, beta: float = 1.0, step_num: int = None, verbose: bool = False) -> float:
sim = make_adjoint_sim(param, beta, unfold=False) # non-differentiable if `unfold=True`
task_name = "inv_des"
if step_num:
task_name += f"_step_{step_num}"
sim_data = web.run(sim, task_name=task_name, verbose=verbose)
mode_power, dip_power = fom(sim_data)
fom_val = mode_power / dip_power
penalty_weight = 0.1
penalty_val = penalty(param, beta)
J = fom_val - penalty_weight * penalty_val
return J, [sim_data, mode_power, dip_power, penalty_val]
# Function to calculate the objective function value and its gradient with respect to the design parameters.
# Use tidy3d's wrapped ag.value_and_grad() for it's auxiliary data functionality
obj_grad = value_and_grad(obj, has_aux=True)
In the following cell, we define some functions to save the optimization progress and load a previous optimization from the file.
# where to store history
history_fname = "misc/qe_light_coupler_autograd.pkl"
def save_history(history_dict: dict) -> None:
"""Convenience function to save the history to file."""
with open(history_fname, "wb") as file:
pickle.dump(history_dict, file)
def load_history() -> dict:
"""Convenience method to load the history from file."""
with open(history_fname, "rb") as file:
history_dict = pickle.load(file)
return history_dict
Then, we will start a new optimization or load the parameters of a previous one.
# initialize adam optimizer with starting parameters
optimizer = optax.adam(learning_rate=learning_rate)
try:
history_dict = load_history()
opt_state = history_dict["opt_states"][-1]
params = history_dict["params"][-1]
opt_state = optimizer.init(params)
num_iters_completed = len(history_dict["params"])
print("Loaded optimization checkpoint from file.")
print(f"Found {num_iters_completed} iterations previously completed out of {max_iter} total.")
if num_iters_completed < max_iter:
print("Will resume optimization.")
else:
print("Optimization completed, will return results.")
except FileNotFoundError:
params = anp.array(init_par)
opt_state = optimizer.init(params)
history_dict = dict(
values=[],
coupl_eff=[],
penalty=[],
params=[],
gradients=[],
opt_states=[opt_state],
data=[],
beta=[],
)
WARNING:2025-07-26 16:10:43,499:jax._src.xla_bridge:967: An NVIDIA GPU may be present on this machine, but a CUDA-enabled jaxlib is not installed. Falling back to cpu.
In the optimization loop, we will gradually increase the projection parameter beta to eliminate intermediary permittivity values. At each iteration, we record the design parameters and the optimization history to restore them as needed.
iter_done = len(history_dict["values"])
if iter_done < max_iter:
# small # of iters for quick testing
for i in range(iter_done, max_iter):
print(f"Iteration = ({i + 1} / {max_iter})")
plt.subplots(1, 1, figsize=(3, 2))
plt.imshow(np.flipud(1 - params.T), cmap="gray", vmin=0, vmax=1)
plt.axis("off")
plt.show()
# Compute gradient and current objective function value.
beta_i = i // iter_steps + beta_min
(value, gradient), data = obj_grad(params, beta=beta_i, step_num=(i + 1))
sim_data_i, mode_power_i, dip_power_i, penalty_val_i = [data[0]] + [
dat._value for dat in data[1:]
]
# Outputs.
print(f"\tbeta = {beta_i}")
print(f"\tJ = {value:.4e}")
print(f"\tgrad_norm = {np.linalg.norm(gradient):.4e}")
print(f"\tpenalty = {penalty_val_i:.3f}")
print(f"\tmode power = {mode_power_i:.3f}")
print(f"\tdip power = {dip_power_i:.3f}")
print(f"\tcoupling efficiency = {mode_power_i / dip_power_i:.3f}")
# Compute and apply updates to the optimizer based on gradient (-1 sign to maximize obj_fn).
updates, opt_state = optimizer.update(-gradient, opt_state, params)
params = optax.apply_updates(params, updates)
# Cap parameters between 0 and 1.
params = anp.minimum(params, 1.0)
params = anp.maximum(params, 0.0)
# Save history.
history_dict["values"].append(value)
history_dict["coupl_eff"].append(mode_power_i / dip_power_i)
history_dict["penalty"].append(penalty_val_i)
history_dict["params"].append(params)
history_dict["beta"].append(beta_i)
history_dict["gradients"].append(gradient)
history_dict["opt_states"].append(opt_state)
# history_dict["data"].append(sim_data_i) # Uncomment to store data, can create large files.
save_history(history_dict)
Iteration = (1 / 100)
beta = 1.0 J = 7.1432e-02 grad_norm = 6.8739e-02 penalty = 1.000 mode power = 473.968 dip power = 2764.752 coupling efficiency = 0.171 Iteration = (2 / 100)
beta = 1.0 J = 2.2832e-01 grad_norm = 7.1512e-02 penalty = 1.000 mode power = 1002.394 dip power = 3053.089 coupling efficiency = 0.328 Iteration = (3 / 100)
beta = 1.0 J = 3.7482e-01 grad_norm = 6.4898e-02 penalty = 1.000 mode power = 1478.833 dip power = 3114.501 coupling efficiency = 0.475 Iteration = (4 / 100)
beta = 1.0 J = 4.9571e-01 grad_norm = 5.6425e-02 penalty = 1.000 mode power = 1935.575 dip power = 3249.175 coupling efficiency = 0.596 Iteration = (5 / 100)
beta = 1.0 J = 5.8980e-01 grad_norm = 4.6824e-02 penalty = 1.000 mode power = 2418.556 dip power = 3506.185 coupling efficiency = 0.690 Iteration = (6 / 100)
beta = 2.0 J = 6.9596e-01 grad_norm = 5.4160e-02 penalty = 1.000 mode power = 3059.636 dip power = 3843.981 coupling efficiency = 0.796 Iteration = (7 / 100)
beta = 2.0 J = 7.4070e-01 grad_norm = 3.8978e-02 penalty = 1.000 mode power = 3716.945 dip power = 4421.261 coupling efficiency = 0.841 Iteration = (8 / 100)
beta = 2.0 J = 7.7138e-01 grad_norm = 3.0304e-02 penalty = 1.000 mode power = 4429.873 dip power = 5083.755 coupling efficiency = 0.871 Iteration = (9 / 100)

beta = 2.0 J = 7.9249e-01 grad_norm = 2.9056e-02 penalty = 1.000 mode power = 5169.262 dip power = 5791.995 coupling efficiency = 0.892 Iteration = (10 / 100)

beta = 2.0 J = 8.0856e-01 grad_norm = 2.8136e-02 penalty = 1.000 mode power = 6042.956 dip power = 6651.128 coupling efficiency = 0.909 Iteration = (11 / 100)

beta = 3.0 J = 7.9742e-01 grad_norm = 9.7527e-02 penalty = 1.000 mode power = 7003.191 dip power = 7803.999 coupling efficiency = 0.897 Iteration = (12 / 100)

beta = 3.0 J = 8.3259e-01 grad_norm = 3.7221e-02 penalty = 0.999 mode power = 8407.922 dip power = 9016.226 coupling efficiency = 0.933 Iteration = (13 / 100)
beta = 3.0 J = 8.2696e-01 grad_norm = 6.7464e-02 penalty = 0.999 mode power = 8736.356 dip power = 9425.743 coupling efficiency = 0.927 Iteration = (14 / 100)
beta = 3.0 J = 8.1778e-01 grad_norm = 1.0335e-01 penalty = 0.999 mode power = 8016.955 dip power = 8736.591 coupling efficiency = 0.918 Iteration = (15 / 100)
beta = 3.0 J = 8.3701e-01 grad_norm = 7.7907e-02 penalty = 0.998 mode power = 7685.024 dip power = 8203.539 coupling efficiency = 0.937 Iteration = (16 / 100)
beta = 4.0 J = 8.1204e-01 grad_norm = 1.5668e-01 penalty = 0.983 mode power = 5820.384 dip power = 6393.784 coupling efficiency = 0.910 Iteration = (17 / 100)
beta = 4.0 J = 8.4011e-01 grad_norm = 1.0337e-01 penalty = 0.977 mode power = 7501.458 dip power = 7998.690 coupling efficiency = 0.938 Iteration = (18 / 100)
beta = 4.0 J = 8.6124e-01 grad_norm = 2.8364e-02 penalty = 0.971 mode power = 10468.018 dip power = 10923.463 coupling efficiency = 0.958 Iteration = (19 / 100)
beta = 4.0 J = 8.5361e-01 grad_norm = 7.5763e-02 penalty = 0.963 mode power = 13775.781 dip power = 14501.615 coupling efficiency = 0.950 Iteration = (20 / 100)
beta = 4.0 J = 8.5295e-01 grad_norm = 8.1482e-02 penalty = 0.956 mode power = 16346.014 dip power = 17233.051 coupling efficiency = 0.949 Iteration = (21 / 100)
beta = 5.0 J = 8.7218e-01 grad_norm = 5.7052e-02 penalty = 0.875 mode power = 17111.887 dip power = 17829.989 coupling efficiency = 0.960 Iteration = (22 / 100)
beta = 5.0 J = 8.8005e-01 grad_norm = 5.3833e-02 penalty = 0.865 mode power = 17308.501 dip power = 17908.051 coupling efficiency = 0.967 Iteration = (23 / 100)
beta = 5.0 J = 8.8289e-01 grad_norm = 3.2505e-02 penalty = 0.854 mode power = 15082.259 dip power = 15576.252 coupling efficiency = 0.968 Iteration = (24 / 100)
beta = 5.0 J = 8.8113e-01 grad_norm = 4.4331e-02 penalty = 0.843 mode power = 12419.322 dip power = 12863.968 coupling efficiency = 0.965 Iteration = (25 / 100)
beta = 5.0 J = 8.7947e-01 grad_norm = 6.3651e-02 penalty = 0.832 mode power = 12087.040 dip power = 12555.809 coupling efficiency = 0.963 Iteration = (26 / 100)
beta = 6.0 J = 8.8584e-01 grad_norm = 7.8859e-02 penalty = 0.732 mode power = 10924.212 dip power = 11390.265 coupling efficiency = 0.959 Iteration = (27 / 100)
beta = 6.0 J = 8.9808e-01 grad_norm = 3.3468e-02 penalty = 0.722 mode power = 17336.079 dip power = 17867.154 coupling efficiency = 0.970 Iteration = (28 / 100)
beta = 6.0 J = 9.0230e-01 grad_norm = 7.8044e-02 penalty = 0.712 mode power = 25590.844 dip power = 26288.327 coupling efficiency = 0.973 Iteration = (29 / 100)
beta = 6.0 J = 8.9802e-01 grad_norm = 9.3922e-02 penalty = 0.702 mode power = 26559.148 dip power = 27429.898 coupling efficiency = 0.968 Iteration = (30 / 100)
beta = 6.0 J = 8.9534e-01 grad_norm = 7.9459e-02 penalty = 0.694 mode power = 21200.802 dip power = 21975.043 coupling efficiency = 0.965 Iteration = (31 / 100)
beta = 7.0 J = 8.9894e-01 grad_norm = 1.4495e-01 penalty = 0.610 mode power = 11024.127 dip power = 11483.994 coupling efficiency = 0.960 Iteration = (32 / 100)
beta = 7.0 J = 9.0821e-01 grad_norm = 7.0287e-02 penalty = 0.604 mode power = 15566.298 dip power = 16071.417 coupling efficiency = 0.969 Iteration = (33 / 100)
beta = 7.0 J = 9.0284e-01 grad_norm = 1.1942e-01 penalty = 0.597 mode power = 24449.286 dip power = 25399.992 coupling efficiency = 0.963 Iteration = (34 / 100)
beta = 7.0 J = 9.0576e-01 grad_norm = 1.2081e-01 penalty = 0.591 mode power = 25232.320 dip power = 26150.739 coupling efficiency = 0.965 Iteration = (35 / 100)
beta = 7.0 J = 9.1589e-01 grad_norm = 4.2125e-02 penalty = 0.585 mode power = 18147.493 dip power = 18623.626 coupling efficiency = 0.974 Iteration = (36 / 100)
beta = 8.0 J = 9.1102e-01 grad_norm = 1.3288e-01 penalty = 0.522 mode power = 8422.290 dip power = 8743.769 coupling efficiency = 0.963 Iteration = (37 / 100)
beta = 8.0 J = 9.1466e-01 grad_norm = 1.2887e-01 penalty = 0.518 mode power = 11193.142 dip power = 11582.000 coupling efficiency = 0.966 Iteration = (38 / 100)
beta = 8.0 J = 9.2233e-01 grad_norm = 4.5024e-02 penalty = 0.514 mode power = 22909.328 dip power = 23528.628 coupling efficiency = 0.974 Iteration = (39 / 100)
beta = 8.0 J = 9.1957e-01 grad_norm = 1.8263e-01 penalty = 0.510 mode power = 33641.288 dip power = 34663.037 coupling efficiency = 0.971 Iteration = (40 / 100)
beta = 8.0 J = 9.2188e-01 grad_norm = 9.1393e-02 penalty = 0.505 mode power = 29094.673 dip power = 29920.135 coupling efficiency = 0.972 Iteration = (41 / 100)
beta = 9.0 J = 9.1973e-01 grad_norm = 1.7000e-01 penalty = 0.458 mode power = 10998.133 dip power = 11390.796 coupling efficiency = 0.966 Iteration = (42 / 100)
beta = 9.0 J = 9.2859e-01 grad_norm = 9.8428e-02 penalty = 0.454 mode power = 11288.366 dip power = 11589.890 coupling efficiency = 0.974 Iteration = (43 / 100)
beta = 9.0 J = 9.2298e-01 grad_norm = 1.3906e-01 penalty = 0.450 mode power = 16924.833 dip power = 17484.737 coupling efficiency = 0.968 Iteration = (44 / 100)
beta = 9.0 J = 9.2668e-01 grad_norm = 1.0958e-01 penalty = 0.446 mode power = 28103.075 dip power = 28934.711 coupling efficiency = 0.971 Iteration = (45 / 100)
beta = 9.0 J = 9.2947e-01 grad_norm = 1.2422e-01 penalty = 0.441 mode power = 35342.692 dip power = 36301.386 coupling efficiency = 0.974 Iteration = (46 / 100)
beta = 10.0 J = 9.1725e-01 grad_norm = 2.0425e-01 penalty = 0.402 mode power = 22519.909 dip power = 23521.792 coupling efficiency = 0.957 Iteration = (47 / 100)
beta = 10.0 J = 9.3295e-01 grad_norm = 8.7255e-02 penalty = 0.397 mode power = 27879.178 dip power = 28662.293 coupling efficiency = 0.973 Iteration = (48 / 100)
beta = 10.0 J = 9.2987e-01 grad_norm = 1.6063e-01 penalty = 0.393 mode power = 36241.082 dip power = 37392.982 coupling efficiency = 0.969 Iteration = (49 / 100)
beta = 10.0 J = 9.3010e-01 grad_norm = 1.5227e-01 penalty = 0.388 mode power = 34755.844 dip power = 35869.977 coupling efficiency = 0.969 Iteration = (50 / 100)
beta = 10.0 J = 9.3480e-01 grad_norm = 8.6082e-02 penalty = 0.383 mode power = 24952.972 dip power = 25642.153 coupling efficiency = 0.973 Iteration = (51 / 100)
beta = 11.0 J = 9.2062e-01 grad_norm = 2.6132e-01 penalty = 0.353 mode power = 14742.606 dip power = 15421.940 coupling efficiency = 0.956 Iteration = (52 / 100)
beta = 11.0 J = 9.3850e-01 grad_norm = 6.0557e-02 penalty = 0.351 mode power = 30944.033 dip power = 31783.785 coupling efficiency = 0.974 Iteration = (53 / 100)
beta = 11.0 J = 9.2657e-01 grad_norm = 4.5544e-01 penalty = 0.349 mode power = 62661.433 dip power = 65175.091 coupling efficiency = 0.961 Iteration = (54 / 100)
beta = 11.0 J = 9.3726e-01 grad_norm = 1.3739e-01 penalty = 0.344 mode power = 26083.433 dip power = 26843.055 coupling efficiency = 0.972 Iteration = (55 / 100)
beta = 11.0 J = 9.3110e-01 grad_norm = 2.7552e-01 penalty = 0.340 mode power = 14073.962 dip power = 14582.365 coupling efficiency = 0.965 Iteration = (56 / 100)
beta = 12.0 J = 9.3442e-01 grad_norm = 2.0789e-01 penalty = 0.318 mode power = 10793.581 dip power = 11171.070 coupling efficiency = 0.966 Iteration = (57 / 100)
beta = 12.0 J = 9.3674e-01 grad_norm = 2.0010e-01 penalty = 0.316 mode power = 24160.809 dip power = 24951.189 coupling efficiency = 0.968 Iteration = (58 / 100)
beta = 12.0 J = 9.3609e-01 grad_norm = 4.0679e-01 penalty = 0.314 mode power = 70509.692 dip power = 72879.455 coupling efficiency = 0.967 Iteration = (59 / 100)
beta = 12.0 J = 9.3791e-01 grad_norm = 2.0113e-01 penalty = 0.311 mode power = 41804.340 dip power = 43143.020 coupling efficiency = 0.969 Iteration = (60 / 100)
beta = 12.0 J = 9.4025e-01 grad_norm = 2.5264e-01 penalty = 0.307 mode power = 25748.521 dip power = 26517.867 coupling efficiency = 0.971 Iteration = (61 / 100)
beta = 13.0 J = 9.4298e-01 grad_norm = 1.9770e-01 penalty = 0.289 mode power = 18771.299 dip power = 19314.514 coupling efficiency = 0.972 Iteration = (62 / 100)
beta = 13.0 J = 9.3831e-01 grad_norm = 2.4655e-01 penalty = 0.286 mode power = 36051.354 dip power = 37283.141 coupling efficiency = 0.967 Iteration = (63 / 100)
beta = 13.0 J = 9.4770e-01 grad_norm = 3.0916e-01 penalty = 0.284 mode power = 73330.091 dip power = 75124.741 coupling efficiency = 0.976 Iteration = (64 / 100)
beta = 13.0 J = 9.4116e-01 grad_norm = 2.3562e-01 penalty = 0.281 mode power = 48064.009 dip power = 49586.843 coupling efficiency = 0.969 Iteration = (65 / 100)
beta = 13.0 J = 9.4345e-01 grad_norm = 2.5314e-01 penalty = 0.279 mode power = 34732.187 dip power = 35758.010 coupling efficiency = 0.971 Iteration = (66 / 100)
beta = 14.0 J = 9.5072e-01 grad_norm = 1.4767e-01 penalty = 0.264 mode power = 28125.287 dip power = 28783.696 coupling efficiency = 0.977 Iteration = (67 / 100)
beta = 14.0 J = 9.4194e-01 grad_norm = 2.4715e-01 penalty = 0.262 mode power = 46559.660 dip power = 48091.621 coupling efficiency = 0.968 Iteration = (68 / 100)
beta = 14.0 J = 9.4917e-01 grad_norm = 2.2277e-01 penalty = 0.260 mode power = 72396.961 dip power = 74239.709 coupling efficiency = 0.975 Iteration = (69 / 100)
beta = 14.0 J = 9.4340e-01 grad_norm = 2.4728e-01 penalty = 0.258 mode power = 50687.983 dip power = 52298.049 coupling efficiency = 0.969 Iteration = (70 / 100)
beta = 14.0 J = 9.4637e-01 grad_norm = 2.1213e-01 penalty = 0.256 mode power = 46727.818 dip power = 48073.883 coupling efficiency = 0.972 Iteration = (71 / 100)
beta = 15.0 J = 9.4793e-01 grad_norm = 2.0206e-01 penalty = 0.245 mode power = 43807.749 dip power = 45051.273 coupling efficiency = 0.972 Iteration = (72 / 100)
beta = 15.0 J = 9.4802e-01 grad_norm = 2.3269e-01 penalty = 0.243 mode power = 65613.204 dip power = 67481.891 coupling efficiency = 0.972 Iteration = (73 / 100)
beta = 15.0 J = 9.4520e-01 grad_norm = 2.0955e-01 penalty = 0.241 mode power = 58289.876 dip power = 60136.353 coupling efficiency = 0.969 Iteration = (74 / 100)
beta = 15.0 J = 9.4843e-01 grad_norm = 1.9381e-01 penalty = 0.239 mode power = 59574.966 dip power = 61270.094 coupling efficiency = 0.972 Iteration = (75 / 100)
beta = 15.0 J = 9.4856e-01 grad_norm = 1.8808e-01 penalty = 0.237 mode power = 71769.585 dip power = 73817.117 coupling efficiency = 0.972 Iteration = (76 / 100)
beta = 16.0 J = 9.4920e-01 grad_norm = 2.2412e-01 penalty = 0.227 mode power = 34792.815 dip power = 35798.471 coupling efficiency = 0.972 Iteration = (77 / 100)
beta = 16.0 J = 9.5233e-01 grad_norm = 1.1844e-01 penalty = 0.225 mode power = 49022.100 dip power = 50286.898 coupling efficiency = 0.975 Iteration = (78 / 100)
beta = 16.0 J = 9.4676e-01 grad_norm = 4.5962e-01 penalty = 0.223 mode power = 112223.050 dip power = 115803.635 coupling efficiency = 0.969 Iteration = (79 / 100)
beta = 16.0 J = 9.5146e-01 grad_norm = 2.6840e-01 penalty = 0.222 mode power = 24794.677 dip power = 25465.193 coupling efficiency = 0.974 Iteration = (80 / 100)
beta = 16.0 J = 9.4763e-01 grad_norm = 2.8706e-01 penalty = 0.221 mode power = 20580.707 dip power = 21223.601 coupling efficiency = 0.970 Iteration = (81 / 100)
beta = 17.0 J = 9.4846e-01 grad_norm = 2.7118e-01 penalty = 0.213 mode power = 26519.913 dip power = 27347.167 coupling efficiency = 0.970 Iteration = (82 / 100)
beta = 17.0 J = 9.4705e-01 grad_norm = 2.4277e-01 penalty = 0.211 mode power = 83580.160 dip power = 86326.033 coupling efficiency = 0.968 Iteration = (83 / 100)
beta = 17.0 J = 9.4165e-01 grad_norm = 4.2922e-01 penalty = 0.210 mode power = 107209.997 dip power = 111366.379 coupling efficiency = 0.963 Iteration = (84 / 100)
beta = 17.0 J = 9.5012e-01 grad_norm = 2.7870e-01 penalty = 0.210 mode power = 26200.887 dip power = 26981.020 coupling efficiency = 0.971 Iteration = (85 / 100)
beta = 17.0 J = 9.4240e-01 grad_norm = 3.2850e-01 penalty = 0.209 mode power = 22240.250 dip power = 23088.709 coupling efficiency = 0.963 Iteration = (86 / 100)
beta = 18.0 J = 9.4756e-01 grad_norm = 2.9047e-01 penalty = 0.202 mode power = 21835.585 dip power = 22562.989 coupling efficiency = 0.968 Iteration = (87 / 100)
beta = 18.0 J = 9.4655e-01 grad_norm = 2.8581e-01 penalty = 0.201 mode power = 44635.553 dip power = 46177.909 coupling efficiency = 0.967 Iteration = (88 / 100)
beta = 18.0 J = 9.4568e-01 grad_norm = 1.4660e+00 penalty = 0.198 mode power = 191151.713 dip power = 197978.584 coupling efficiency = 0.966 Iteration = (89 / 100)
beta = 18.0 J = 9.0565e-01 grad_norm = 7.1548e-01 penalty = 0.200 mode power = 7787.385 dip power = 8413.092 coupling efficiency = 0.926 Iteration = (90 / 100)
beta = 18.0 J = 9.1608e-01 grad_norm = 5.4755e-01 penalty = 0.200 mode power = 3829.103 dip power = 4090.553 coupling efficiency = 0.936 Iteration = (91 / 100)
beta = 19.0 J = 9.1000e-01 grad_norm = 4.0796e-01 penalty = 0.196 mode power = 3154.019 dip power = 3393.009 coupling efficiency = 0.930 Iteration = (92 / 100)
beta = 19.0 J = 8.9532e-01 grad_norm = 4.8212e-01 penalty = 0.196 mode power = 3168.027 dip power = 3462.783 coupling efficiency = 0.915 Iteration = (93 / 100)
beta = 19.0 J = 9.1045e-01 grad_norm = 3.6817e-01 penalty = 0.196 mode power = 3353.528 dip power = 3605.939 coupling efficiency = 0.930 Iteration = (94 / 100)
beta = 19.0 J = 9.3083e-01 grad_norm = 2.9490e-01 penalty = 0.195 mode power = 3787.969 dip power = 3985.947 coupling efficiency = 0.950 Iteration = (95 / 100)
beta = 19.0 J = 9.4441e-01 grad_norm = 2.1215e-01 penalty = 0.194 mode power = 4620.248 dip power = 4793.893 coupling efficiency = 0.964 Iteration = (96 / 100)
beta = 20.0 J = 9.3738e-01 grad_norm = 2.9252e-01 penalty = 0.188 mode power = 5972.530 dip power = 6246.091 coupling efficiency = 0.956 Iteration = (97 / 100)
beta = 20.0 J = 9.4350e-01 grad_norm = 2.2733e-01 penalty = 0.186 mode power = 9200.513 dip power = 9562.867 coupling efficiency = 0.962 Iteration = (98 / 100)
beta = 20.0 J = 9.5092e-01 grad_norm = 1.1442e-01 penalty = 0.184 mode power = 15828.774 dip power = 16330.019 coupling efficiency = 0.969 Iteration = (99 / 100)
beta = 20.0 J = 9.4448e-01 grad_norm = 1.1112e-01 penalty = 0.182 mode power = 30118.514 dip power = 31287.115 coupling efficiency = 0.963 Iteration = (100 / 100)
beta = 20.0 J = 9.3400e-01 grad_norm = 1.4951e-01 penalty = 0.179 mode power = 60020.849 dip power = 63053.450 coupling efficiency = 0.952
Ultimately, we get all the information to assess the optimization results.
obj_vals = np.array(history_dict["values"])
ce_vals = np.array(history_dict["coupl_eff"])
pen_vals = np.array(history_dict["penalty"])
final_par_density = history_dict["params"][-1]
final_beta = history_dict["beta"][-1]
# just to inspect design at different iterations
def unfold_params(params):
params = np.concatenate((np.fliplr(np.copy(params)), params), axis=1)
return params
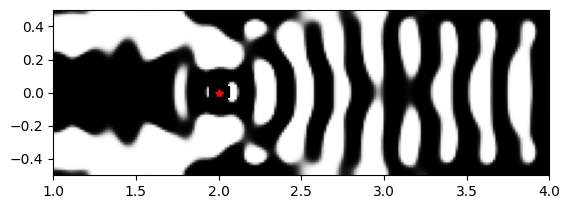
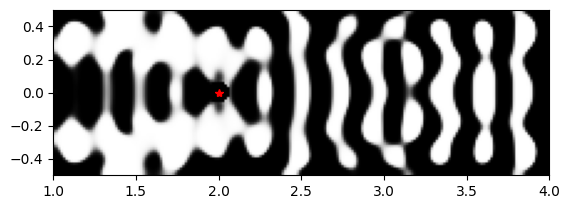
params1 = history_dict["params"][32]
params1_full = pre_process(params1, beta=final_beta)
params1_full = include_constant_regions(
params1_full, circ_center=[qe_pos.center[0], qe_pos.center[1]], circ_radius=non_etch_r
)
params1_full = unfold_params(params1_full)
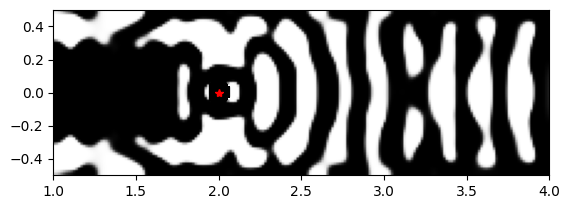
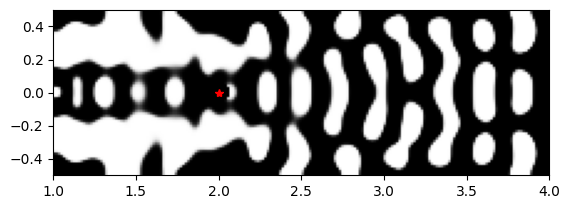
params2 = history_dict["params"][-1]
params2_full = pre_process(params2, beta=final_beta)
params2_full = include_constant_regions(
params2_full, circ_center=[qe_pos.center[0], qe_pos.center[1]], circ_radius=non_etch_r
)
params2_full = unfold_params(params2_full)
plt.imshow(
1 - np.flipud(params1_full.T),
cmap="gray",
vmin=0,
vmax=1,
extent=[wg_length, cr_l + wg_length, -cr_w / 2, cr_w / 2],
)
plt.plot(dp_source.center[0], 0, "r*")
plt.show()
plt.imshow(
1 - np.flipud(params2_full.T),
cmap="gray",
vmin=0,
vmax=1,
extent=[wg_length, cr_l + wg_length, -cr_w / 2, cr_w / 2],
)
plt.plot(dp_source.center[0], 0, "r*")
plt.show()
Results¶
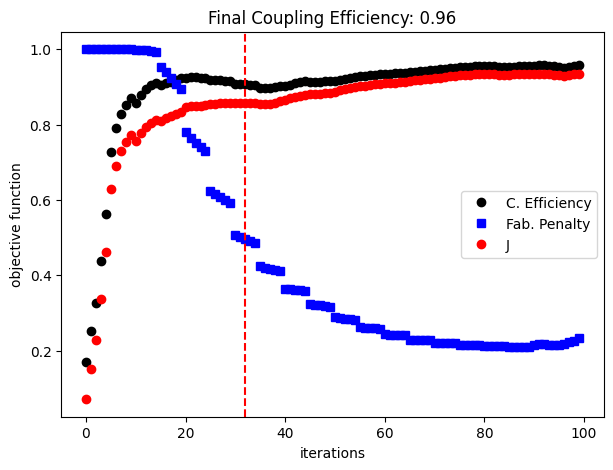
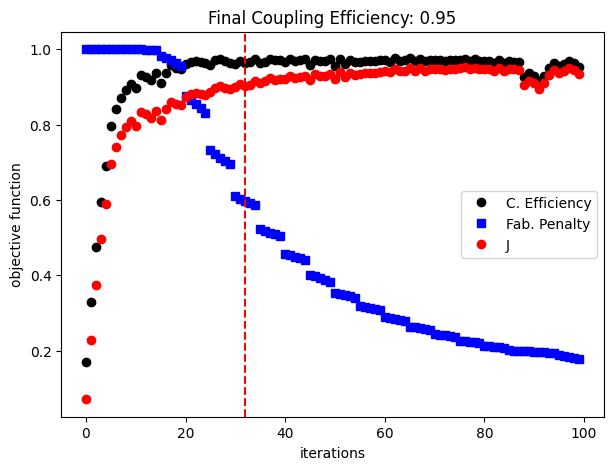
The following figure shows how coupling efficiency and the fabrication penalty have evolved along the optimization process. The coupling efficiency quickly rises above 0.8, and along the binarization process, we can observe two large drops before a more stable final optimization stage. The formation of resonant modes sensitive to the small structural changes can potentially explain this behavior. The discontinuities in the fabrication penalty curve are caused by the increments in the projection parameter beta at each 5 iterations.
fig, ax = plt.subplots(1, 1, figsize=(7, 5))
ax.plot(ce_vals, "ko", label="C. Efficiency")
ax.plot(pen_vals, "bs", label="Fab. Penalty")
ax.plot(history_dict["values"], "ro", label="J")
ax.set_xlabel("iterations")
ax.set_ylabel("objective function")
ax.set_title(f"Final Coupling Efficiency: {ce_vals[-1]:.2f}")
ax.axvline(x=32, color="r", linestyle="--")
ax.legend()
plt.show()
Interestingly, fully binarizing the design from iteration 32 produced a device with great coupling efficiency (~97%), but minimal purcell enhancement
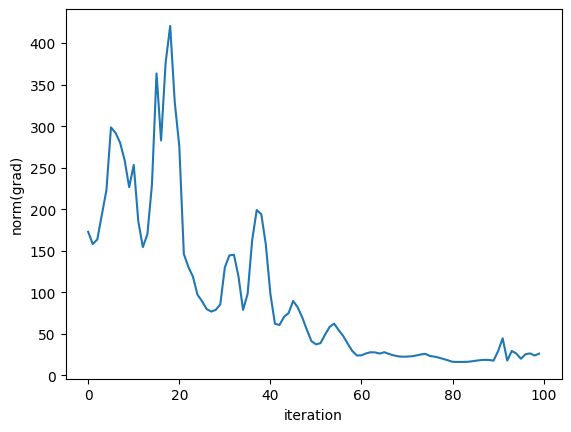
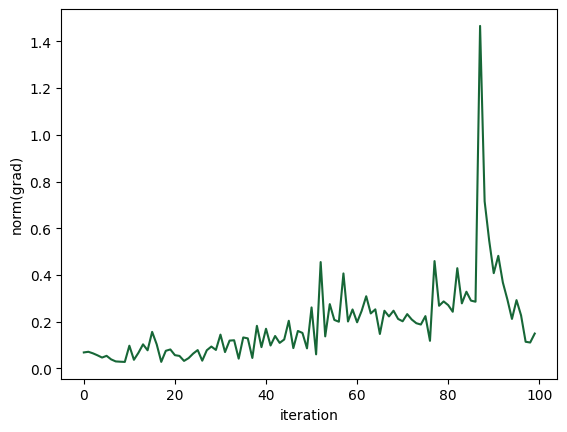
plt.plot([np.linalg.norm(grad) for grad in history_dict["gradients"]])
plt.ylabel("norm(grad)")
plt.xlabel("iteration")
Text(0.5, 0, 'iteration')
Makes a nice animation of the design parameters and gradient evolution during the optimization
import matplotlib.animation as animation
from mpl_toolkits.axes_grid1 import make_axes_locatable
fig, axs = plt.subplots(nrows=2, ncols=1)
gradients = history_dict["gradients"]
params = history_dict["params"]
gradients = [unfold_params(grad).T for grad in gradients]
params = [unfold_params(init_par).T] + [unfold_params(1.0 - p).T for p in params]
div = make_axes_locatable(axs[1])
div0 = make_axes_locatable(axs[0])
cax = div.append_axes("top", size="5%", pad=0.05)
cax0 = div0.append_axes("bottom", size="5%", pad=0.05)
cax0.axis("off")
def animate(i):
im_g = axs[1].imshow(
gradients[i], interpolation="none", vmin=np.min(gradients[i]), vmax=np.max(gradients[i])
)
axs[0].imshow(params[i], interpolation="none", cmap="gray", vmin=0, vmax=1)
axs[1].axis("off")
axs[0].axis("off")
cax.cla()
fig.colorbar(im_g, cax=cax, orientation="horizontal").ax.xaxis.set_ticks_position("top")
axs[0].set_title(f"iteration {i}")
anim = animation.FuncAnimation(fig, animate, frames=100, blit=False, interval=500)
anim.save("autograd_anim.mp4", fps=2.0)
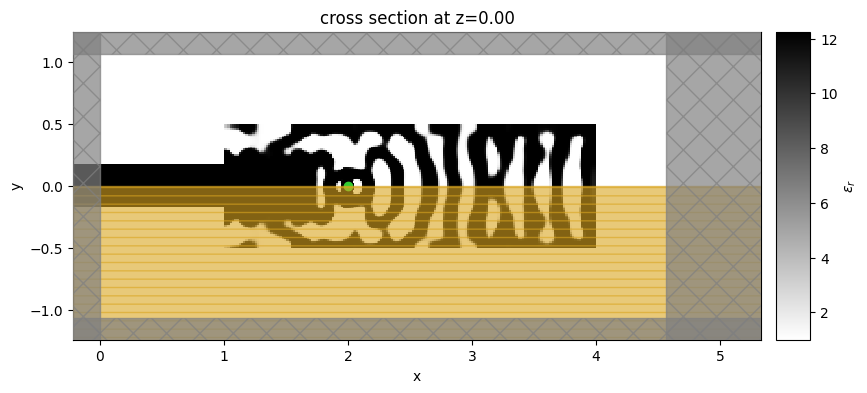
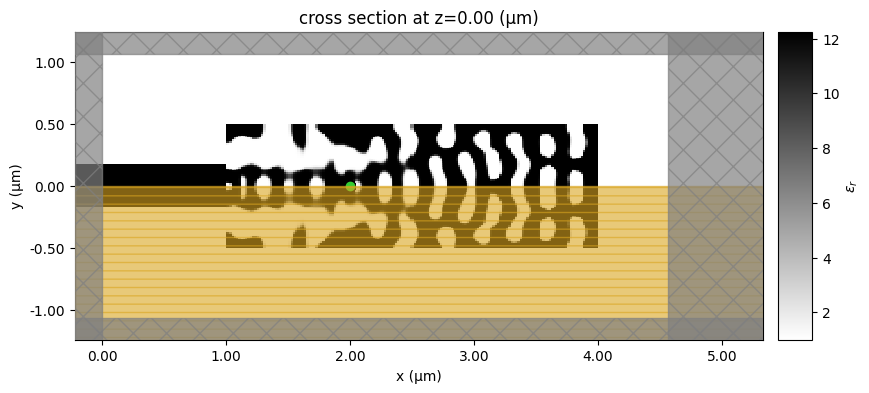
Interestingly, the final quantum emitter light extractor resembles a nanocavity, even though we have considered only the coupling efficiency into the output waveguide in the optimization. We have DBR mirrors on both sides of the dipole. However, on the left side, the mirror has only a few periods and partially reflects the radiation, which couples to the output waveguide.
# here, removing substrate improved performance, but also blue-shifted cavity resonance a bit.
fig, ax = plt.subplots(1, figsize=(10, 4))
# Substrate layer.
substrate = td.Structure(
geometry=td.Box.from_bounds(
rmin=(-eff_inf, -eff_inf, -eff_inf), rmax=(eff_inf, eff_inf, -wg_thick / 2)
),
medium=td.Medium(permittivity=1.0),
)
sim_final = make_adjoint_sim(params2, beta=final_beta, unfold=True)
sim_final = sim_final.updated_copy(monitors=[field_monitor_xy, mode_monitor] + field_monitor)
sim_final.plot_eps(
z=0,
source_alpha=0,
monitor_alpha=0,
ax=ax,
)
plt.show()
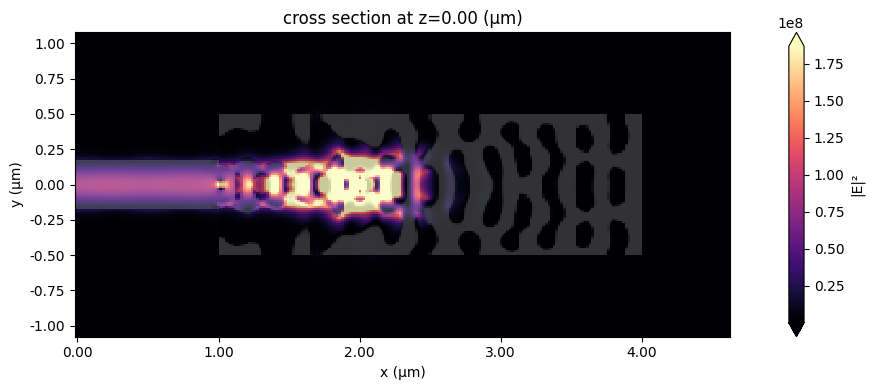
To better understand the resultant design, let's simulate the final structure to obtain its spectral response and field distribution.
sim_data_final = web.run(sim_final, task_name="final QE light extractor")
18:56:12 CEST Created task 'final QE light extractor' with task_id 'fdve-7b5a7f2b-9dda-46bc-8519-0af1e82273c8' and task_type 'FDTD'.
View task using web UI at 'https://tidy3d.simulation.cloud/workbench?taskId=fdve-7b5a7f2b-9d da-46bc-8519-0af1e82273c8'.
Task folder: 'default'.
Output()
18:56:14 CEST Maximum FlexCredit cost: 0.058. Minimum cost depends on task execution details. Use 'web.real_cost(task_id)' to get the billed FlexCredit cost after a simulation run.
18:56:15 CEST status = queued
To cancel the simulation, use 'web.abort(task_id)' or 'web.delete(task_id)' or abort/delete the task in the web UI. Terminating the Python script will not stop the job running on the cloud.
Output()
18:56:27 CEST starting up solver
running solver
Output()
18:56:36 CEST early shutoff detected at 24%, exiting.
status = postprocess
Output()
18:56:41 CEST status = success
18:56:43 CEST View simulation result at 'https://tidy3d.simulation.cloud/workbench?taskId=fdve-7b5a7f2b-9d da-46bc-8519-0af1e82273c8'.
Output()
18:56:47 CEST loading simulation from simulation_data.hdf5
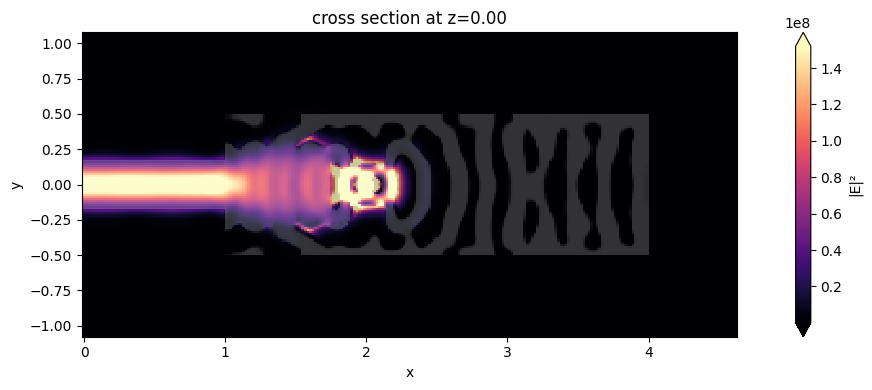
In this cavity-like system, the extraction efficiency of photons from the QE into the collection waveguide mode is proportional to $\beta\times C_{wg}$, where the $\beta$-factor quantifies the fraction of the QE spontaneous emission emitted in the cavity mode, and $C_{wg}$ is the fraction of the cavity photons coupled to the guided mode A. Enderlin, Y. Ota, R. Ohta, N. Kumagai, S. Ishida, S. Iwamoto, and Y. Arakawa, "High guided mode–cavity mode coupling for an efficient extraction of spontaneous emission of a single quantum dot embedded in a photonic crystal nanobeam cavity," Phys. Rev. B 86, 075314 (2012) DOI: 10.1103/PhysRevB.86.075314. By the field distribution image below, we can see a cavity mode resonance, which should increase the Purcell factor at the QE position, thus contributing to a higher $\beta$-factor. At the same time, the partial reflection mirror at the left side was potentially optimized to adjust $C_{wg}$.
f, ax1 = plt.subplots(1, 1, figsize=(12, 4), tight_layout=True)
sim_data_final.plot_field("field_xy", "E", "abs^2", z=0, ax=ax1, f=freqs[0])
plt.show()
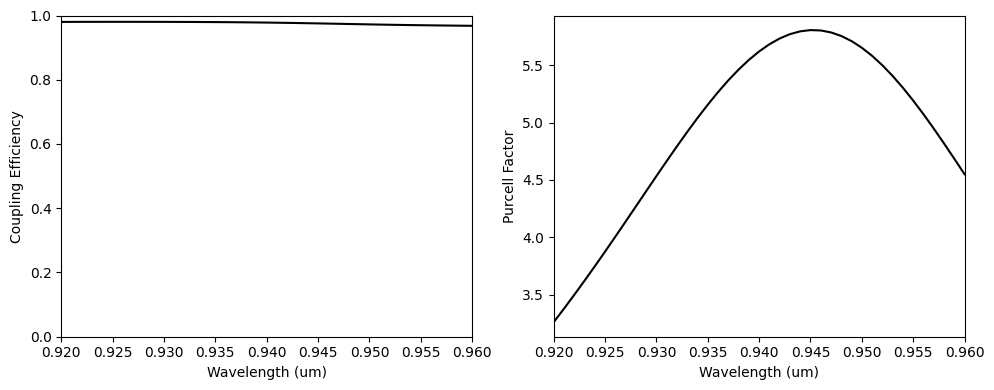
To conclude, we will calculate the final coupling efficiency and the cavity Purcell value. The coupling efficiency is above 80% along an extensive wavelength range, and we have confirmed the Purcell enhancement.
# Coupling efficiency.
mode_amps = sim_data_final["mode_monitor"].amps.sel(direction="-", mode_index=0)
mode_power = np.abs(mode_amps) ** 2
dip_power = np.zeros(n_wl)
for i in range(len(field_monitor)):
field_mon = sim_data_final[f"field_monitor_{i}"]
dip_power += np.abs(field_mon.flux)
coup_eff = mode_power / dip_power
# Purcell factor.
bulk_power = ((2 * np.pi * freqs) ** 2 / (12 * np.pi)) * (td.MU_0 * n_wg / td.C_0)
bulk_power = bulk_power * 2 ** (2 * np.sum(np.abs(sim_final.symmetry)))
purcell = dip_power / bulk_power
f, (ax1, ax2) = plt.subplots(1, 2, figsize=(10, 4), tight_layout=True)
ax1.plot(wl_range, coup_eff, "-k")
ax1.set_xlabel("Wavelength (um)")
ax1.set_ylabel("Coupling Efficiency")
ax1.set_ylim(0, 1)
ax1.set_xlim(wl - bw / 2, wl + bw / 2)
ax2.plot(wl_range, purcell, "-k")
ax2.set_xlabel("Wavelength (um)")
ax2.set_ylabel("Purcell Factor")
ax2.set_xlim(wl - bw / 2, wl + bw / 2)
plt.show()
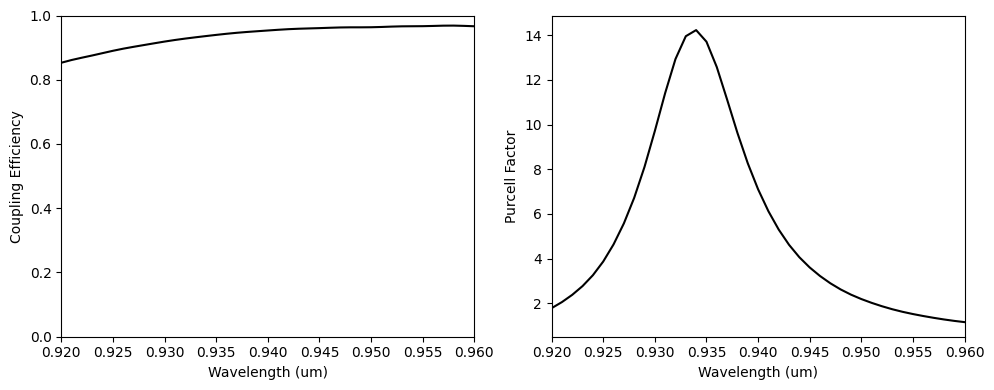
print(np.max(coup_eff.values))
print(np.min(coup_eff.values))
0.9685581762335904 0.8529465434212032
Export to GDS¶
The Simulation object has the .to_gds_file convenience function to export the final design to a GDS file. In addition to a file name, it is necessary to set a cross-sectional plane (z = 0 in this case) on which to evaluate the geometry, a frequency to evaluate the permittivity, and a permittivity_threshold to define the shape boundaries in custom mediums. See the GDS export notebook for a detailed example on using .to_gds_file and other GDS related functions.
# make the misc/ directory to store the GDS file if it doesn't exist already
import os
if not os.path.exists("./misc/"):
os.mkdir("./misc/")
sim_final.to_gds_file(
fname="./misc/inv_des_light_extractor_autograd.gds",
z=0,
permittivity_threshold=(eps_max + eps_min) / 2,
frequency=freq,
)